Содержание

• Шагать

Тригонометрическое уравнение - это уравнение с одной или несколькими тригонометрическими функциями переменной тригонометрической кривой x. Решение относительно x означает нахождение значений тригонометрических кривых, тригонометрические функции которых приводят к истинности тригонометрического уравнения.

• Ответы или значения кривых решения выражаются в градусах или радианах. Примеры:

х = Пи / 3; х = 5Пи / 6; х = 3Пи / 2; х = 45 градусов; x = 37,12 градуса; x = 178,37 градуса

• Примечание. На единичной окружности тригонометрические функции любой кривой равны тригонометрическим функциям соответствующего угла. Единичный круг определяет все тригонометрические функции переменной кривой x. Он также используется в качестве доказательства при решении основных тригонометрических уравнений и неравенств.
• Примеры тригонометрических уравнений:
  • грех х + грех 2х = 1/2; загар х + кроватка х = 1,732;
  • cos 3x + sin 2x = cos x; 2sin 2x + cos x = 1.

1. Единичный круг.
   • Это круг с радиусом = 1, где O - начало координат. Единичный круг определяет 4 основные тригонометрические функции переменной кривой x, которая вращается вокруг нее против часовой стрелки.
   • Когда кривая со значением x изменяется на единичной окружности, выполняется:
   • Горизонтальная ось OAx определяет тригонометрическую функцию f (x) = cos x.
   • Вертикальная ось OBy определяет тригонометрическую функцию f (x) = sin x.
   • Вертикальная ось AT определяет тригонометрическую функцию f (x) = tan x.
   • Горизонтальная ось BU определяет тригонометрическую функцию f (x) = cot x.

• Единичный круг также используется для решения основных тригонометрических уравнений и стандартных тригонометрических неравенств с учетом различных положений кривой x на окружности.

Шагать

1. Разберитесь в методе решения.
   • Чтобы решить тригонометрическое уравнение, вы конвертируете его в одно или несколько основных тригонометрических уравнений. Решение тригонометрических уравнений в конечном итоге приводит к решению 4 основных тригонометрических уравнений.
2. Умейте решать основные тригонометрические уравнения.
   • Есть 4 основных тригонометрических уравнения:
   • грех х = а; соз х = а
   • загар х = а; детская кроватка x = a
   • Вы можете решить основные тригонометрические уравнения, изучая различные положения кривой x на тригонометрическом круге и используя таблицу тригонометрического преобразования (или калькулятор). Чтобы полностью понять, как решать эти и аналогичные базовые тригонометрические уравнения, прочтите следующую книгу: «Тригонометрия: решение тригонометрических уравнений и неравенств» (Amazon E-book 2010).
   • Пример 1. Решите относительно sin x = 0,866. Таблица преобразования (или калькулятор) дает ответ: x = Pi / 3. Тригонометрический круг дает другую кривую (2Pi / 3) с тем же значением для синуса (0,866). Тригонометрический круг также дает бесконечное количество ответов, называемых расширенными ответами.
   • x1 = Pi / 3 + 2k.Pi и x2 = 2Pi / 3. (Ответов в течение периода (0, 2Pi))
   • x1 = Pi / 3 + 2k Pi и x2 = 2Pi / 3 + 2k Pi. (Подробные ответы).
   • Пример 2. Решаем: cos x = -1/2. Калькуляторы дают x = 2 Pi / 3. Тригонометрический круг также дает x = -2Pi / 3.
   • x1 = 2Pi / 3 + 2k.Pi и x2 = - 2Pi / 3. (Ответы за период (0, 2Pi))
   • x1 = 2Pi / 3 + 2k Pi и x2 = -2Pi / 3 + 2k.Pi. (Расширенные ответы)
   • Пример 3. Решаем: tan (x - Pi / 4) = 0.
   • х = Пи / 4; (Отвечать)
   • х = Пи / 4 + к Пи; (Расширенный ответ)
   • Пример 4. Решаем: детская кроватка 2x = 1,732. Калькуляторы и тригонометрический круг дают:
   • х = Пи / 12; (Отвечать)
   • х = Пи / 12 + k Пи; (Расширенные ответы)
3. Изучите преобразования, используемые при решении тригонометрических уравнений.
   • Чтобы преобразовать данное тригонометрическое уравнение в стандартные тригонометрические уравнения, используйте стандартные алгебраические преобразования (факторизация, общий множитель, полиномы ...), определения и свойства тригонометрических функций и тригонометрических тождеств. Существует около 31, 14 из которых являются тригонометрическими тождествами, от 19 до 31, также называемыми тождествами преобразования, потому что они используются при преобразовании тригонометрических уравнений. См. Книгу выше.
   • Пример 5: Тригонометрическое уравнение: sin x + sin 2x + sin 3x = 0 может быть преобразовано в произведение основных тригонометрических уравнений с использованием тригонометрических тождеств: 4cos x * sin (3x / 2) * cos (x / 2) = 0. Необходимо решить следующие основные тригонометрические уравнения: cos x = 0; грех (3х / 2) = 0; и cos (x / 2) = 0.
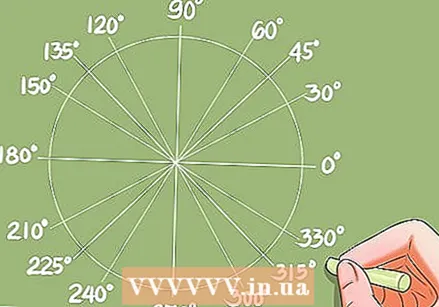4. Найдите кривые, для которых известны тригонометрические функции.
   • Прежде чем вы научитесь решать тригонометрические уравнения, вам нужно знать, как быстро найти кривые, для которых известны тригонометрические функции. Значения преобразования кривых (или углов) можно определить с помощью тригонометрических таблиц или калькулятора.
   • Пример: найти cos x = 0,732. Калькулятор дает решение x = 42,95 градуса. Единичный круг показывает другие кривые с таким же значением косинуса.
5. Нарисуйте дугу ответа на единичном круге.
   • Вы можете создать график, чтобы проиллюстрировать решение на единичном круге. Конечные точки этих кривых - правильные многоугольники на тригонометрической окружности. Несколько примеров:
   • Концы кривой x = Pi / 3 + k. Pi / 2 - квадрат на единичной окружности.
   • Кривые x = Pi / 4 + k.Pi / 3 представлены координатами шестиугольника на единичной окружности.
6. Узнайте, как решать тригонометрические уравнения.
   • Если данное тригонометрическое уравнение содержит только одну тригонометрическую функцию, решите его как стандартное тригонометрическое уравнение. Если данное уравнение содержит две или более тригонометрических функции, существует 2 метода решения, в зависимости от вариантов преобразования уравнения.
     • А. Способ 1.
   • Преобразуйте тригонометрическое уравнение в произведение вида: f (x) .g (x) = 0 или f (x) .g (x) .h (x) = 0, где f (x), g (x) и h (x) - основные тригонометрические уравнения.
   • Пример 6. Решаем: 2cos x + sin 2x = 0. (0 x 2Pi)
   • Решение. Замените sin 2x в уравнении, используя тождество: sin 2x = 2 * sin x * cos x.
   • cos x + 2 * sin x * cos x = 2cos x * (sin x + 1) = 0. Затем решите две стандартные тригонометрические функции: cos x = 0 и (sin x + 1) = 0.
   • Пример 7. Решите: cos x + cos 2x + cos 3x = 0. (0 x 2Pi)
   • Решение. Преобразуйте это в произведение, используя тригонометрические тождества: cos 2x (2cos x + 1) = 0. Теперь решите 2 основных тригонометрических уравнения: cos 2x = 0 и (2cos x + 1) = 0.
   • Пример 8. Решаем: sin x - sin 3x = cos 2x. (0 x 2Pi)
   • Решение. Преобразуйте это в произведение, используя тригонометрические тождества: -cos 2x * (2sin x + 1) = 0. Теперь решите 2 основных тригонометрических уравнения: cos 2x = 0 и (2sin x + 1) = 0.
     • Б. Подход 2.
   • Преобразует тригонометрическое уравнение в триггерное уравнение с одной уникальной триггерной функцией в качестве переменной. Есть несколько советов, как выбрать подходящую переменную. Общие переменные: sin x = t; cos x = t; cos 2x = t, tan x = t и tan (x / 2) = t.
   • Пример 9. Решите: 3sin ^ 2 x - 2cos ^ 2 x = 4sin x + 7 (0 x 2Pi).
   • Решение. В уравнении замените (cos ^ 2x) на (1 - sin ^ 2x) и упростите уравнение:
   • 3sin ^ 2 x - 2 + 2sin ^ 2 x - 4sin x - 7 = 0. Теперь используйте sin x = t. Уравнение принимает следующий вид: 5t ^ 2 - 4t - 9 = 0. Это квадратное уравнение с двумя корнями: t1 = -1 и t2 = 9/5. Мы можем отклонить второе t2, потому что> 1. Теперь решите: t = sin = -1 -> x = 3Pi / 2.
   • Пример 10. Решаем: tan x + 2 tan ^ 2 x = cot x + 2.
   • Решение. Используйте tan x = t. Преобразуйте данное уравнение в уравнение с t в качестве переменной: (2t + 1) (t ^ 2 - 1) = 0. Решите относительно t из этого произведения, затем решите стандартное тригонометрическое уравнение tan x = t относительно x.
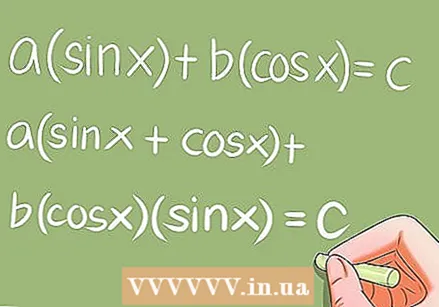7. Решите специальные тригонометрические уравнения.
   • Есть несколько специальных тригонометрических уравнений, которые требуют определенных преобразований. Примеры:
   • а * грех х + Ь * соз х = с; а (грех х + соз х) + Ь * соз х * грех х = с;
   • a * sin ^ 2 x + b * sin x * cos x + c * cos ^ 2 x = 0
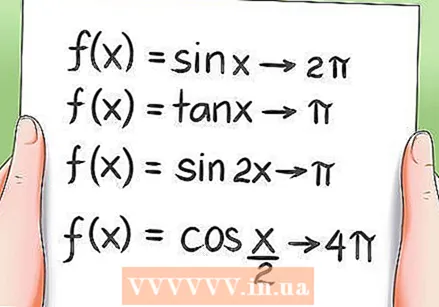8. Изучите периодические свойства тригонометрических функций.
   • Все тригонометрические функции являются периодическими, что означает, что они возвращаются к одному и тому же значению после поворота за период. Примеры:
     • Функция f (x) = sin x имеет период 2Pi.
     • Функция f (x) = tan x имеет период Pi.
     • Функция f (x) = sin 2x имеет период Pi.
     • Функция f (x) = cos (x / 2) имеет период 4Pi.
   • Если период указан в упражнениях / тесте, то вам просто нужно найти кривую (и) x в пределах этого периода.
   • ПРИМЕЧАНИЕ. Решение тригонометрических уравнений сложно и часто приводит к ошибкам и ошибкам. Поэтому ответы следует тщательно проверять. После решения вы можете проверить ответы с помощью графического калькулятора для прямого представления данного тригонометрического уравнения R (x) = 0. Ответы (в виде квадратного корня) даны в десятичных разрядах. Например, Pi имеет значение 3,14.